Research Summary: Challenges Associated With Modelling Outburst Floods From Moraine-Dammed Glacial Lakes

by Matt Westoby ^{1, 2}
— August 13, 2014

¹Geography, Northumbria University, Newcastle-upon-Tyne, UK

²Department of Geography and Earth Sciences, Aberystwyth University, UK

Introduction

Climatic change is causing the widespread retreat of glacier ice at the global scale. Observed glacier recession and associated mass loss is particularly dramatic in many high-mountain regions, such as the Hindu Kush Himalaya, the South American Cordillera and the European Alps, where glacial meltwater forms the headwaters of some of the world’s largest rivers, in turn sustaining many millions of people.

Figure 1. Supraglacial melt ponds on the surface of Ngozumpa Glacier, Khumbu Himal, Nepal. With continued expansion, these ponds may coalesce to form a ‘proto’ moraine-dammed lake, which, if it doesn’t drain, will go on to create a fully-formed moraine-dammed lake containing many millions of cubic metres of water. (Credit: Matt Westoby)

Glaciers effectively act as enormous conveyor belts which are capable of transporting astounding quantities of debris, sourced from avalanching and rockfall and the scour of the valley sides and floor. Upon reaching the glacier margin, this debris is deposited to form a ‘moraine’. Moraines are composed of unconsolidated sediment (and sometimes buried ice) and can reach many tens of metres in height. As a parent glacier recedes, these moraines are exposed. Should a moraine form a continuous loop and remain relatively stable, glacial meltwater may pond in the deglaciated basin between the moraine and the receding glacier terminus, and will gradually fill up (much like a giant bath tub.) Alternatively, if the surface gradient of the glacier tongue is shallow enough, melt ponds will form on the glacier tongue, which, following expansion and coalescence, may also result in the development of a fully-formed glacial lake. The largest lake in Nepal, Tsho Rolpa, was estimated to impound ~10⁷ m³of water¹. To put this in context, that’s enough water to fill 4000 Olympic-size swimming pools.

Figure 2. Moraine-dammed lakes in the Nepal Himalaya: (A) Tsho Rolpa, which impounded over 100 million m3 at the turn of the last century (27°51’31.62″N, 86°28’45.34″E) and (B) Dig Tsho, which was breached in 1985, forming a GLOF that destroyed bridges, trails, buildings and agricultural land, and caused a number of fatalities (27°52’24.81″N, 86°35’19.35″E). (Credit: Google Earth)

Many moraine-dammed lakes pose a very real threat to downstream communities. If the impounding moraine fails, for example due to an impulse wave triggered by a rock or ice avalanche that overtops the moraine and initiates breaching, the escaping floodwaters will form a Glacial Lake Outburst Flood, or ‘GLOF’ ². Historical GLOFs have caused many fatalities and have wiped out entire settlements, valuable agricultural land, trails, roads and bridges, and communications infrastructure which were located in the flood path^3,4. They represent a very real threat to downstream communities; a threat that is ever-increasing as high-mountain regions become more populated and the number of moraine-dammed lakes increases.

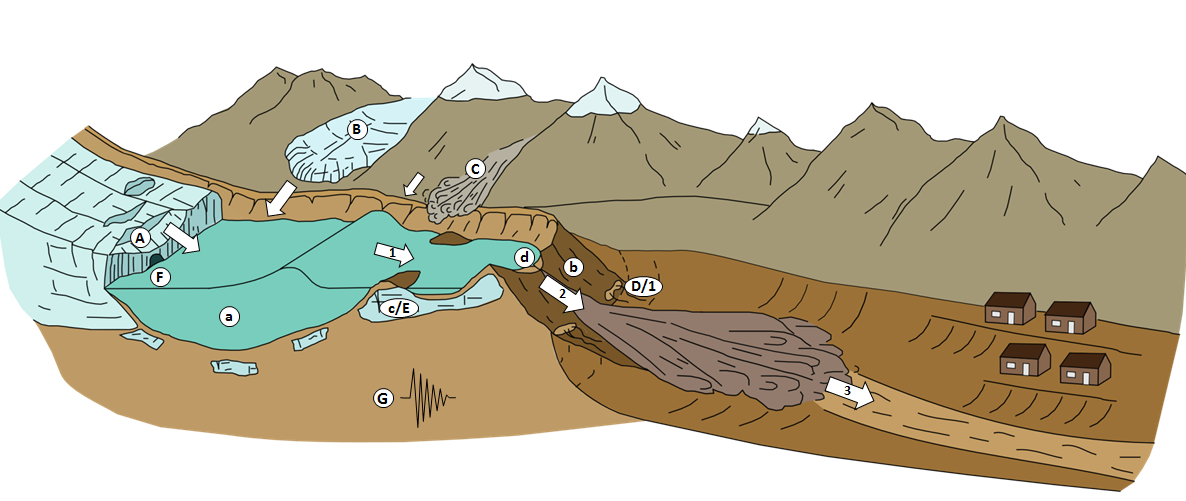
Figure 3. Schematic of a hazardous moraine-dammed glacial lake. Potential triggers, conditioning factors, and key ‘phases’ in a GLOF event are highlighted. Potential triggers include: (A) contact glacier calving; (B) icefall from hanging glaciers; (C) rock/ice/snow avalanches; (D) dam settlement and/or piping; (E) ice-cored moraine degradation; (F) rapid input of water from supra-, en-, or subglacial (including subaqueous) sources; (G) seismicity Conditioning factors for dam failure include (a) large lake volume; (b) low width-to-height dam ratio; (c) degradation of buried ice in the moraine structure; (d) limited dam freeboard. Key stages of a GLOF include (1) propagation of displacement or seiche waves in the lake, and/or piping through the dam; (2) breach initiation and breach formation; (3) propagation of resultant flood wave(s) down-valley. Adapted from Richardson and Reynolds (2000a) – figure source: Fig. 3, Westoby et al. (2014a).

Research Aim

The aim of our recent review² was to evaluate the methods available to researchers and hazard assessment professionals for modelling the different stages of a GLOF. The purpose of the modelling might be to reconstruct a historical GLOF, or to investigate the impact of a potential future GLOF. Whilst the former may provide valuable insights into outburst flood dynamics through the comparison of modelled patterns of flow depth, inundation extent, and erosion and deposition with field evidence, the latter are central to the development of effective disaster mitigation strategies, including the timely evacuation of people from flood-prone areas downstream. The research presented in the paper was undertaken primarily from an extensive search of the academic literature, and also draws upon the lead author’s experience of visiting field sites in the Nepal Himalaya and reconstructing a handful of GLOFs for their doctoral research at the Centre for Glaciology at Aberystwyth University, UK.

Dam Breach Modelling

Whilst the research touches upon the methods available to model GLOF triggering events, such as lake impulse wave propagation, the initial focus of the paper is on the methods available to simulate the breaching of a moraine dam. These methods can be broadly categorised as: empirical models, analytical models, and fully physically based numerical models. Empirical models are derived from test case studies or observed dam failures, but are not process-based. They are only able to provide the user with an estimated peak breach discharge, and a time to peak discharge, and require prior knowledge of the moraine geometry (e.g. its height, width, length) and/or the glacial lake (e.g. it’s volume, depth, and surface area), which can be plugged into a simple equation. Analytical or parametric models are slightly more advanced, in that they may be semi-physically based, but typically assume that the time taken for the breach to reach its maximum size is known. For a historical moraine breach, this information might be available, but is often not.

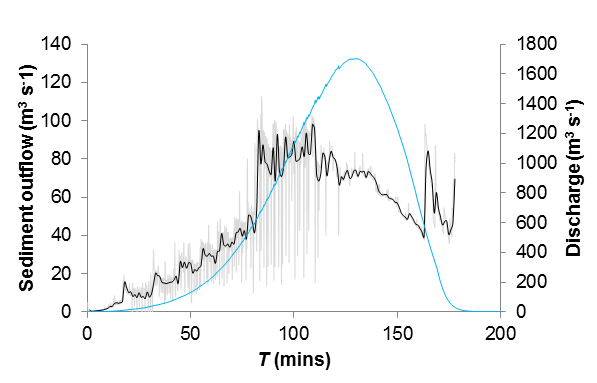
Figure 4. Rates of sediment evacuation (Qs) during moraine breaching: in this instance an experimental reconstruction of the 1985 Dig Tsho GLOF event using the HR-BREACH dam-breach model. Sediment outflow fluctuates significantly between successive 10-second time steps as the result of periodic discrete breach wall failure events, which deliver considerable, though short-lived ‘pulses’ of sediment to the developing outflow channel. (Source: Fig. 7, Westoby et al., 2014a)

The most advanced models are fully physically based numerical solvers that incorporate process equations for modelling breach expansion and breach flow using data describing key sediment properties such as its material strength or cohesion, porosity, internal friction angle, and the grain size distribution of sediment comprising the moraine, as well as flow hydraulics models^5,6. Such data are typically available only through detailed (not to mention often logistically challenging!) field investigation, although it might be argued that their grounding in geotechnical and flow hydraulics theory make them highly appropriate for modelling moraine breaching.

Outburst Flood Modelling

Once the user has obtained a breach hydrograph, the next stage is to simulate the downstream passage of the outburst flood. Once again, a range of models that vary in complexity are available. The simplest models are GIS-based flow routing algorithms that transfer flow from a predefined starting zone to adjacent cells, based predominantly on the slope angle of an underlying Digital Elevation Model (DEM)⁷. Such algorithms are simple to use, but are unable to model many key and dynamic physical characteristics of the flood. One-dimensional models, such as the widely used HEC-RAS code, are based on the shallow water St-Venant equations, but are only capable of modelling flow in a single dimension (i.e. downstream), and cannot account for transversal or vertical variations in flow direction. These models require the user to set up sequential cross-sections to represent the valley topography, with the model interpolating flow depths, velocities and inundation patterns from one cross-section to the next.

Figure 5. Maps of GLOF flow depth, flow velocity and maximum mobile clast size (left, centre and right columns, respectively) for selected time steps. Breach outflow hydrograph displayed in Figure 9. For context, a Structure-from-Motion-derived DTM of the floodplain, extracted at 1 m2, is displayed beneath the data. For scale, inset tick marks are spaced at 200 m intervals (Source: Fig. 9, Westoby et al., 2014, Earth Surface Proc. Landforms).

Two-dimensional hydrodynamic models can simulate multi-directional (x,y) and multi-channel flow and are therefore able to capture some of the more complex dynamics of GLOFs, such as increased water heights at the outside of channel bends (termed ‘flow superelevation’), and flow recirculation zones. These codes require the user to supply a DEM to serve as the topographic modelling domain, or grid. The level of detail, or spatial discretisation, of this grid may have a significant effect on the GLOF travel time, flow depth, and inundation extent, such that coarser grids might overestimate the inundated area, whilst finer grids will refine it. Other higher-order hydrodynamic models include fully 3-D solvers, or mesh-free methods such as smoothed-particle hydrodynamics⁸, however, such codes are incredibly computationally demanding and are not currently in widespread use.

Key challenges that modellers face here stem in large part from the incredible complexity of these flows. Many entrain and deposit large volumes of sediment (as well as vegetation), which bulks the flow and changes its viscosity and rheology, and subsequently its behaviour and mobility⁹. GLOFs are capable of transforming from largely sediment-free, clearwater flows to debris flows within a kilometre of their source, which cannot be adequately simulated using standard Newtonian fluid laws. This represents a significant modelling challenge, and many modellers treat the GLOF as a single-phase, water-only problem for the sake of simplicity and the computational demand associated with using higher-order codes. Assessment of the accuracy of such models also requires the availability of pre- and post-flood DEMs, which allow the modeller to see whether the modelled patterns of erosion and deposition match those observed in reality for documented GLOFs¹⁰. However, these data are rarely available due to the logistical (and financial) challenges associated with producing repeat topographic surveys of often remote and largely inaccessible valleys, as well as predicting if and when a given moraine will fail.

Figure 6. Imja Tsho moraine-dammed lake, Khumbu Himal, Nepal. This lake has grown from a network of supraglacial melt ponds within two decades and is currently the subject of much research by the scientific community to establish the likelihood of moraine failure and the release of a GLOF. It is worth noting the extensive terminal moraine complex, which has been proven to contain buried glacier ice (Source: ‘Glaciers online’ (http://www.swisseduc.ch/glaciers/index-de.html), photograph credit MJ Hambrey).

Challenges Posed by Contemporary and Future Climate Change

Rates of glacier recession are predicted to increase in coming decades on a scale without any historical precedent. A major challenge is predicting when and where new lakes will form, as well as their rate of growth, potential impoundment volume, and how rates of expansion contribute to the potential future GLOF hazard posed by these lakes. Such uncertainty abounds in the modelling chain described above, and is also present in, for example, the parameterisation of a numerical dam-breach model where tweaking individual input parameters may produce differing breach hydrographs, which in turn could be associated with differing patterns of flood inundation, depths and timings. Unfortunately, this is far from an exact science. However, modellers, and in turn potential flood-affected communities, should benefit from the gradual improvements in the affordability and availability of computational resources, advanced dam-breach and hydrodynamic codes, topographic data, and advances in our process-based understanding of the conditions required for lake formation, the moraine breaching process and outburst flood simulation.

References

¹ Sakai A, Chikita K and Yamada T (2000) Expansion of a moraine-dammed glacial lake, Tsho Rolpa, in Rolwaling Himal, Nepal Himalaya. Limnology and Oceanography 45, 1401-1408.
² Westoby MJ, Glasser NF, Brasington J, Hambrey MJ, Quincey DJ and Reynolds JM (2014) Modelling outburst floods from moraine-dammed glacial lakes. Earth-Sciences Reviews 134, 137-159.
³Vuichard D and Zimmerman M (1987) The 1985 catastrophic drainage of a moraine-dammed lake, Khumbu Himal, Nepal: cause and consequences. Mountain Research and Development 7, 91-110.
⁴Watanabe T and Rothacher D (1994) The 1994 Lugge Tsho Glacial Lake Outburst Flood, Bhutan Himalaya. Mountain Research and Development 16, 77-81.
⁵ Westoby MJ, Glasser NF, Hambrey MJ, Brasington J, Reynolds JM and Hassan MAAM (2014) Reconstructing historic Glacial Lake Outburst Floods through numerical modelling and geomorphological assessment: Extreme events in the Himalaya. Earth Surface Processes and Landforms, DOI: 10.1002/esp.3617
⁶Worni R, Stoffel M, Huggel C, Volz C, Casteller A and Luckman B (2012) Analysis and dynamic modelling of a moraine failure and glacier lake outburst flood at Ventisquero Negro, Patagonian Andes (Argentina). Journal of Hydrology 444-445, 134-145.
⁷ Huggel C, Haeberli W, Kääb A, Bieri D and Richardson S (2004) An assessment procedure for glacial hazards in the Swiss Alps. Canadian Geotechnical Journal 41, 1068=1083.
⁸ Huang Y, Dai Z, Zhang W and Chen Z (2011) Visual simulation of landslide fluidized movement based on smoothed particle hydrodynamics. Natural Hazards 59, 1225-1238.
⁹ Iverson RM, Reid ME, Logan M, LaHusen RG, Godt JW and Griswold JP (2011) Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment. Nature Geoscience 4, 116-121.
¹⁰ Carrivick JL, Manville V, Graettinger A and Cronin SJ (2010) Coupled fluid dynamics-sediment treansport modelling of a Crater lake break-out lahar: Mt Ruapehu, New Zealand. Journal of Hydrology 388, 399-413.